I robot nell’ambiente produttivo

Per analizzare l’impatto dell’introduzione dei robot in ambiente produttivo, può essere utile studiare il modello di Georg Graetz e Guy Michaels, che mostra la relazione tra robot e lavoro. Per semplificare le cose, sono stati presi in considerazione due settori diversi:

• Il primo utilizza una funzione di produzione CES per combinare robot e lavoro;
• Il secondo usa soltanto lavoro.

Un settore vede l’utilizzo congiunto di due input diversi, i robot e i lavoratori umani, mentre l’altro settore ha come input di produzione soltanto la manodopera. Supponiamo inoltre che i consumatori abbiamo un’utilità descritta tramite una funzione CES e che vengano consumati interamente tutti gli output generati.

Quindi l’utilità dei consumatori sarà:

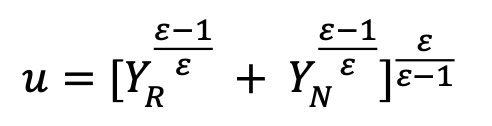
Per semplicità si considerino i consumatori soggetti a vincoli di budget. Viene indicata con ε l’elasticità di sostituzionenel consumo tra gli output dei due settori. La quantità di robot usata nella produzione viene indicata con R e si suppone che i robot siano perfettamente elastici al prezzo p e con L è rappresentata la quantità di lavoro impiegata nella produzione degli output e si intende perfettamente inelastica e perfettamente mobile tra i due settori.

Il lavoro nei due settori sarà denominato 𝐿_𝑅 e 𝐿_𝑁 nel caso in cui sia relativo al settore con i robot e nel caso in cui invece sia relativo al settore senza robot. Le funzioni di produzione dei due settori sono rispettivamente:

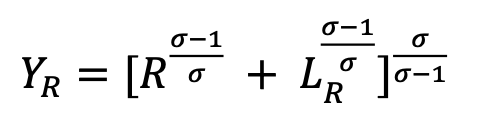
e

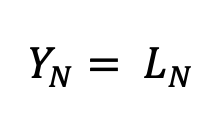
dove σ rappresenta l’elasticità di sostituzione tra robot e lavoro nel settore in cui sono presenti i robot.

Attraverso le opportune dimostrazioni si arriva alle seguenti conclusioni:

• Una diminuzione del prezzo dei robot porta ad un aumento della densità dei robot;
• Un aumento nella densità dei robot porta ad un aumento della produttività media del lavoro nel settore in cui sono presenti i robot;
• Con l’aumentare della densità del robot, aumenta anche l’output nel settore che usa i robot rispetto a quello che non utilizza robot;
• L’input di lavoro nel settore che usa robot aumenta (diminuisce) con la densità dei robot se ε > σ (ε < σ). L’allocazione del lavoro tra i vari settori non dipende dalla densità dei robot quando ε = σ.

Per quanto riguarda l’ultima intuizione, una diminuzione nel prezzo dei robot porta le imprese a sostituire i lavoratori con i robot, ma allo stesso tempo aumenta l’output del settore che usa i robot facendo diminuire il prezzo di taleoutput. Questo a sua volta porta i consumatori a comprare più prodotti provenienti dal settore che usa i robot. Ora se l’aumento dell’output non richiede un aumento aggiuntivo di robot o se è necessario un aumento dei lavoratori, dipende da quanto è forte la risposta dell’impresa alla caduta del prezzo dei robot rispetto alla risposta dei consumatori alla caduta del prezzo dell’output (misurati rispettivamente come σ e ε).

Per cercare di spiegare meglio cosa l’elasticità σ e ε rappresentano si può dire che σ cattura le possibilità di sostituzione tra i fattori (robot e lavoro) nella stessa attività oppure la sostituzione tra le diverse attività necessarie per la produzione di un output. Quindi una bassa elasticità sostituzione tra le attività si potrebbe traslare in un basso valore di σ, anche se i robot e i lavoratori sono perfetti sostituti a livello di singola attività.

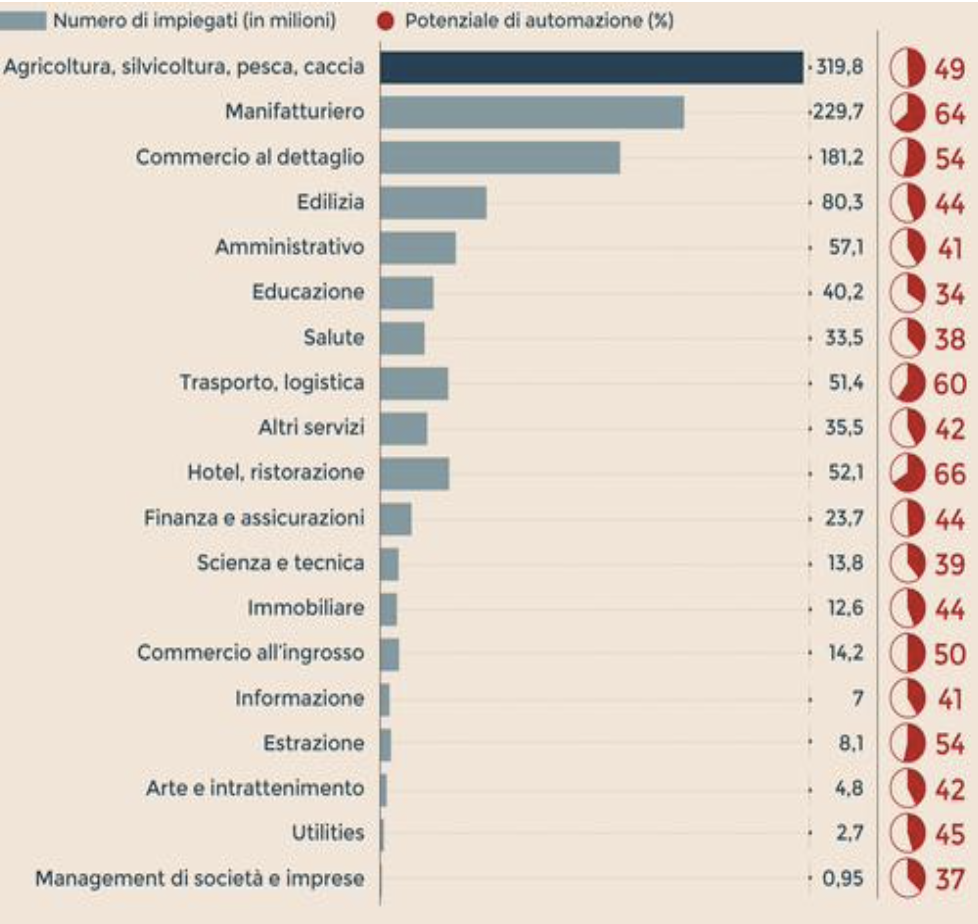
Figura 1 – Tasso di sostituibilità dei lavoratori per settore [Fonte: www.lavocedellelotte.it].

Allo stesso modo, il valore di ε dipende da come sono considerati i due diversi settori descritti nel modello. Se si immaginano i due settori come diversi ma appartenenti alla stessa nazione (ad esempio i settori automotive e costruzione italiani), la sostituzione potrebbe essere limitata e ε potrebbe essere piccolo. Se invece interpretiamo i due settori come uguali ma appartenenti a due nazioni diverse (ad esempio il settore automotive di Germania e Italia),la sostituzione potrebbe essere grande e quindi ε potrebbe assumere un valore elevato.

Conclusioni

In conclusione, questo modello semplificato suggerisce che un aumento nella densità dei robot causata da una caduta del loro prezzo porterebbe ad un aumento del valore aggiunto e della produttività del lavoro. Il dibattito tra glieconomisti è in corso: in linea di massima gli esperti ritengono molto probabile che l’IA contribuirà a un aumento dellaproduttività e degli standard di vita. Tuttavia, è anche probabile che questo avvenga dopo un periodo di transizionedurante il quale molti impieghi attuali cessano di esistere. In particolare, come mostra la figura 12, poiché i lavoratorimeno scolarizzati tendono ad avere mansioni più ripetitive, e poiché i robot tendono a sostituire questo tipo di attività, non sorprende che siano questi lavoratori ad essere sottoposti ad un rischio maggiore di sostituzione.

Bibliografia

• VV. (2018), “Intelligenza artificiale per le imprese: tutti i vantaggi per il futuro delle aziende”,https://www.insidemarketing.it/intelligenza-artificiale-le-imprese-tutti-vantaggi-futuro-delle-aziende/
• VV. (2018), “Intelligenza artificiale, ecco come cambia il business”, https://www.wired.it/economia/business/2017/11/24/intelligenza-artificiale-business-2/
• VV. (2018), “Intelligenza Artificiale: cos’è, come funziona e a cosa serve?”,http://www.intelligenzaartificiale.it/
• VV. (2018), “Reti Neurali”, http://www.intelligenzaartificiale.it/reti-neurali/
• Acemoglu e Restrepo P. (2018), “Modeling Automation”, https://economics.mit.edu/files/14861
• Aghion , Jones. B.E. e Jones C.I. (2017), “Artificial Intelligence and Economic Growth ”,https://web.stanford.edu/~chadj/AI.pdf
• Agrawal , McHale J. e Oettl A., (2018), “ Artificial Intelligence and Recombinant Growth”, http://www.nber.org/chapters/c14024.pdf
• Angelini (2017), “Intelligenza Artificiale e governance. Alcune riflessioni di sistema”, http://www.sipotra.it/wp-content/uploads/2017/10/Intelligenza- artificiale-e-governance.-Alcune-riflessioni-di-sistema.pdf
• Brynjolfsson e McAfee A. (2011), “ Why Workers Are Losing the WarAgainst Machines?”, https://www.theatlantic.com/business/archive/2011/10/why-workers-are-losing-the-war-against-machines/247278/
• Brynjolfsson , Rock D. e Syverson C. (2017), “ Artificial Intelligence and the ModernProductivity Paradox: A Clash of Expectations and Statistics”, http://www.nber.org/chapters/c14007.pdf
• Dorn (2015), “The Rise of the Machines How Computers Have Changed Work”,https://www.ubscenter.uzh.ch/assets/publicpapers/PP4_the_rise_of_the_machines.pdf
• Graetz e Michaels G. (2015), “ Robots at Work”, http://cep.lse.ac.uk/pubs/download/dp1335.pdf
• Harris , Kimson A. e Schwedel A. (2018), “ Labor 2030: the collision of demographics,automation and inequality ”, http://www.bain.com/publications/articles/labor-2030-the-collision-of-demographics-automation-and-inequality.aspx
• Jin Z. (2018), “Artificial Intelligence and Consumer Privacy”, http://www.nber.org/chapters/c14034.pdf
• Korinek e Stiglitz J.E. (2017), “ Artificial Intelligence and Its Implications for Income Distributionand Unemployment” http://www.nber.org/chapters/c14018.pdf
• Maci (2018), “Intelligenza Artificiale, che cos’è e perché trasformerà le aziende”,https://www.economyup.it/startup/intelligenza-artificiale-che-cos-e-e-perche-trasformera-le-aziende/
• Milgrom R. e Tadelis S. (2018), “ How Artificial Intelligence and Machine Learning Can ImpactMarket Design ”, http://www.nber.org/chapters/c14008.pdf
• Purdy e Daugherty P. (2016), “ Why Artificial Intelligence is the Future of Growth”,https://www.accenture.com/t20170927T080049Zw/us-en/_acnmedia/PDF-33/Accenture-Why-AI-is-the-Future-of-Growth.PDFla=en