AI e sistema economico: Modello della crescita ricombinante

Introduzione

I ricercatori Ajay Agrawal, John McHale e Alexander Oettl hanno sviluppato una funzione di produzione della conoscenzacombinatoria e l’hanno incorporata nel classico modello di crescita per esplorare su quali combinazioni le innovazioni nell’IA possano essere più preziose e possano quindi aumentare i tassi di scoperta e, di conseguenza, la crescita economica.

Ovviamente tutto questo fa fronte ad una serie di problemi, quali l’effetto “fishing out” (si pensi ad una zona di pesca dove tutti i pesci migliori siano già stati catturati, in questo caso le innovazioni più importanti sono già state effettuate) o l’effetto “low-hanging fruit” (secondo il quale c’è il rischio di concentrarsi troppo sulla frutta (le innovazioni) più facile da raggiungere, ovvero quella in basso) in quanto le buone idee diventano con il tempo sempre più difficili da trovare.

Man mano che la frontiera tecnologica si espande, diventa sempre più difficile per i singoli ricercatori conoscereabbastanza per trovare le combinazioni di conoscenza che producono nuove idee utili.

Nonostante le prove di un rallentamento della crescita, si nutre speranza nei confronti di queste tecnologie. Inparticolare, a far sperare nel futuro è la recente esplosione della disponibilità dei dati (ovvero i big data) e dei progressi informatici che hanno facilitato l’elaborazione di tali dati. È possibile considerare queste tecnologie come “meta-tecnologie” ossia tecnologie per la produzione di nuove conoscenze. Queste meta-tecnologie offrono il potenziale per superare parzialmente l’effetto fishing- out e i vincoli sociali e istituzionali che limitano l’accesso alla conoscenza.

Questo particolare modello prende in considerazione il modo in cui le conoscenze esistenti vengono combinate al fine di produrre nuove conoscenze sottolineando come l’IA rappresenti uno strumento fondamentale per ricercatori in quanto permette loro di generare conoscenza in spazi di scoperta complessi.

Ricerca e scoperta

Al fine di comprendere meglio questo modello, è molto utile distinguere due tipologie di meta-tecnologie: quelle che aiutano nel processo di ricerca (accesso alla conoscenza) e quelle che aiutano nel processo di scoperta (combinando le conoscenze esistenti per produrre nuove conoscenze).

Per il processo di ricerca, si considerano meta-tecnologie AI–based quelle in grado di soddisfare le seguenti due condizioni:

• La tecnologia deve operare in un contesto in cui i big data hanno aumentato notevolmente la conoscenza potenziale accessibile attraverso il processo di scoperta ed è diventato più difficile per un ricercatore rimanereal passo con tutto il “carico di conoscenza” derivante da queste informazioni;
• La tecnologia deve predire quali frammenti di conoscenza potrebbero essere più rilevanti per il ricercatore.

Per quanto concerne il processo di scoperta, si identificano anche in questo caso due condizioni che l’IA devesoddisfare per essere identificata come meta-tecnologia:

• La tecnologia deve operare in un contesto in cui la conoscenza potenzialmente combinabile per la creazione di nuova conoscenza è soggetta all’esplosione combinatoria;
• La tecnologia deve essere in grado di predire quali combinazioni di conoscenza esistenti produrranno nuove preziose conoscenze.

A titolo esemplificativo, si considerino i seguenti casi in cui le tecnologie di ricerca e scoperta AI-based potrebbero modificare il processo di innovazione.

Ricerca

Meta^α è una società che produce tecnologie AI-based in grado di supportare la ricerca e di identificare documenti scientifici e tracciare l’evoluzione delle idee scientifiche. La società è stata acquisita dalla Chan-Zuckerberg Foundation, che intende renderla disponibile gratuitamente ai ricercatori.

Le tecnologie fornite da questa società soddisfano le due condizioni necessarie ad indentificarle come meta-tecnologie in grado di supportare l’accesso alla conoscenza (quindi durante la fase di ricerca). Infatti:

• La tecnologia opera in un contesto in cui lo stock di articoli scientifici è soggetto a una crescita esponenziale dell’8-9% all’anno;
• La tecnologia di ricerca basata sull’IA fornisce supporto agli scienziati nel processo di analisi dei documenti, individuando quali di questi potrebbero essere più rilevanti e utili per le finalità del ricercatore.

Un altro esempio è fornito dalla tecnologia BenchSci che una tecnologia AI-based capace di identificare i composti usati nei farmaci. Anche in questo caso, la tecnologia soddisfa le due condizioni necessarie ad identificarla come meta-tecnologia in grado di supportare la ricerca. Infatti:

• Le informazioni sui composti sono sparse in milioni di articoli scientifici;
• L’IA alla base della tecnologia è in grado di estrarre informazioni su questi composti, permettendo agli scienziati di identificare in modo più efficace i composti idonei ad essere utilizzati negli esperimenti.

Scoperta

Relativamente al processo di scoperta, Atomwise è una tecnologia basata sulla machine learning impiegata nel processodi scoperta dei composti utili alla produzione di nuovi farmaci sicuri ed efficaci. Questo strumento AI-based può essereidentificato come meta-tecnologia impiegata nel processo di scoperta in quanto soddisfa le due condizioni sopra citate. Infatti:

• Il numero di composti potenziali è soggetto ad esplosione combinatoria;
• L’IA alla base della tecnologia è in grado di predire come le caratteristiche chimiche di base si combinano in caratteristiche più complesse identificando potenziali composti da sottoporre a indagini più dettagliate.

Anche DeepGenomics è una tecnologia basata sulla machine learning ed è in grado di predire cosa accade in una cellula nel momento in cui una variazione genetica alterna il DNA. Anch’essa soddisfa le due condizioni in quanto:

• Le variazioni genotipo-fenotipo sono soggette all’esplosione combinatoria;
• L’IA fornisce supporto alla scoperta prevedendo i risultati dei processi biologici complessi che mettono in luce le variazioni genotipo-fenotipo.

La funzione di produzione della conoscenza

La Figura 1fornisce una panoramica dell’approccio seguito dal modello descritto in questo paragrafo e dal suo rapporto con la classica funzione di produzione della conoscenza di Romer / Jones. Questo modello infatti è una rivisitazione del modello di Romer / Jones di cui si vede una panoramica nella Figura 1.

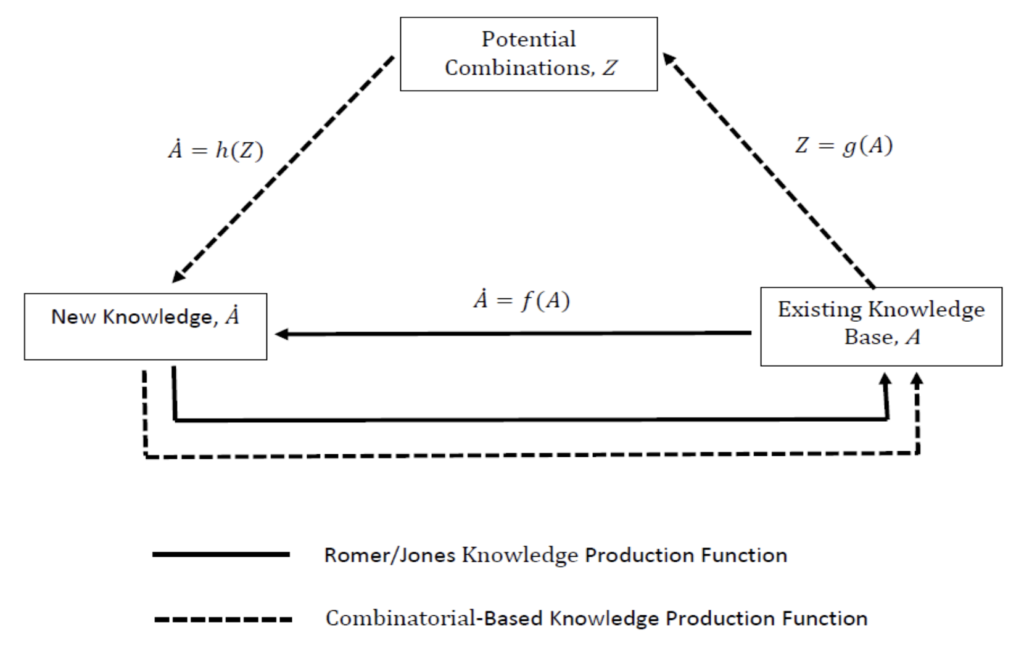
Figura 1 – Modello di Romer/Jones vs. Modello della conosceza combinata [Fonte: Ajay Agrawal, John McHale e Alexander Oettl].

Secondo il modello di Romer / Jones, i ricercatori generano nuova conoscenza basandosi sulla conoscenza di base già esistente. Invece, il nuovo modello, pur essendo simile a quello di Romer / Jones sotto alcuni aspetti, aggiunge un’ulteriore complicazione al processo di creazione della conoscenza. Infatti, come nel modello di Romer / Jones, i ricercatori sfruttano le conoscenze esistenti per generare nuova conoscenza che diventerà parte delle conoscenze di base dal quale potrebbero nascere nuove scoperte. Tuttavia, nel nuovo modello, le conoscenze di base esistenti determinano tutte le possibili combinazioni della conoscenza, la maggior parte delle quali è probabile che non abbia nessun valore.

Il processo di scoperta di nuove conoscenze viene eseguito cercando tra l’enorme numero di combinazioni potenziali.Questo processo di scoperta è supportato dalle meta- tecnologie che, come detto precedentemente, permettono ai ricercatori di identificare combinazioni preziose di conoscenze in contesti dove quest’ultime interagiscono tra loro in modi molto complessi. La conoscenza scoperta si aggiunge così alle conoscenze di base (facendo aumentare il numero delle potenziali combinazioni delle conoscenze di base) impiegate dai ricercatori nel loro lavoro.

In riferimento al modello, si intenda con A lo stock totale di conoscenza presente nel mondo e si assuma (per ora)misurato in modo discreto. Inoltre, si indichi con 𝐴^ϕ (0 < ϕ < 1) la quantità di conoscenza (per ora misurata in modo discreto) a cui un ricercatore ha accesso. Di conseguenza,

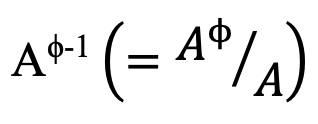
è la frazione dello stock di conoscenza a cui ha accesso un singolo ricercatore. Quanto detto implica che la quota della conoscenza totale accessibile a un singolo ricercatore diminuisce con lo stock totale di conoscenza. Questa è una manifestazione dell’effetto del “carico di conoscenza”, ovvero man mano che cresce lo stock totale di conoscenza diventa più difficile accedere a tutte le conoscenze disponibili.

Si supponga che il parametro di accesso alla conoscenza, ϕ, catturi non solo ciò che un ricercatore conosce in undeterminato momento ma anche la sua capacità di trovare le conoscenze esistenti qualora lo desideri. Quindi, il valore del parametro è influenzato dal grado in cui la conoscenza è disponibile in forma codificata e dalla possibilità di essere trovata, qualora necessario, dai ricercatori.

Secondo questo modello, le innovazioni sono il risultato della combinazione delle conoscenze esistenti per produrrenuove conoscenze. La conoscenza può essere combinata con a idee alla volta, dove a = 0, 1. . . 𝐴^ϕ. Quindi, per un ricercatore individuale, il numero totale di combinazioni possibili delle conoscenze esistenti è dato da:

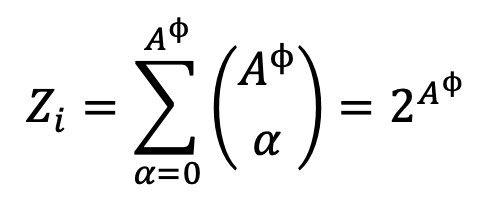(1)

Perciò, si può osservare che il numero totale di combinazioni potenziali, 𝑍i, cresce in modo esponenziale con 𝐴^ϕ. Chiaramente, se anche A crescesse esponenzialmente, 𝑍i crescerà ad un doppio tasso esponenziale. Questa è la causadell’esplosione combinatoria nel modello a cui si aggiunge la crescita esponenziale delle combinazioni potenziali in relazione all’accessibilità della conoscenza.

Finora le variabili A e Zi sono state misurate discretamente; tuttavia, per semplicità, si intendano d’ora in avanticome misurate continuamente.

Identificato il numero totale di combinazioni potenziali, il prossimo passo è quello di specificare come queste combinazioni si trasformano in scoperte (ovvero in nuova conoscenza). Si supponga che un’ampia parte di queste potenziali combinazioni non produca nuova conoscenza utile e che, una parte della conoscenza utile individuata, sia giàstata scoperta (e quindi sia già inclusa in A). In particolare, quest’ultima caratteristica riflette l’effetto fishing-out descritto precedentemente.

La funzione sottostante descrive quanta di questa conoscenza generata si trasforma in nuova conoscenza:

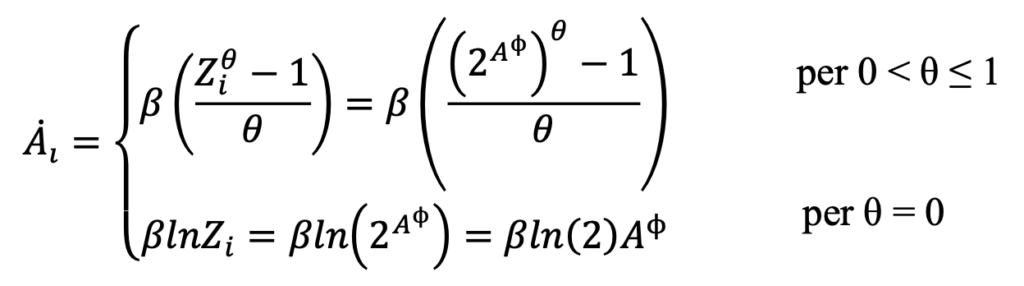(2)

dove β è il parametro che tiene conto di quanta della conoscenza individuata si trasforma in nuova conoscenza e θ è il parametro che tiene conto dell’effetto fishing-out e della complessità dello spazio delle possibili soluzioni. Inoltre, per il caso limite in cui θ = 0, si segue la regola di L’Hôpital in quanto il limite del termine tra parentesi sul lato destro dell’equazione (2) è indeterminato nel caso in cui θ = 0. Perciò, secondo L’Hôpital, il limite in questo caso è pari al limite della derivata del numeratore rispetto a θ diviso il limite della derivata del denominatore rispetto a θ. Questo limite è uguale a ln(2)A^𝛟.

Analizzando nel dettaglio il parametro θ si tenga conto che esso è influenzato da diversi fattori, tra cui:

• La visione pessimistica di alcuni ricercatori che tendono a sottolineare la presenza di vincoli imposti dai fenomeni naturali che limitano la produzione di nuova conoscenza;
• La facilità di scoprire nuove combinazioni utili che, considerando la dimensione e la complessità dello spazio di queste potenziali combinazioni, può portare al needle-in-the-haystack problem (trovare un ago in un pagliaio). Nonostante questo, gli ottimisti tendono a sottolineare come la combinazione di IA e l’aumento della potenza di calcolo dei computer possa aiutare il processo di scoperta;
• Dal percorso seguito dal processo di scoperta fino a quel determinato momento. Grazie all’IA, che fornirà la possibilità di identificare i percorsi migliori da seguire, diminuirà la possibilità di trovarsi in un vicolo cieco della tecnologia.

Dettagliando maggiormente il modello, si supponga ora che siano presenti all’interno del sistema economico LAricercatori che operano indipendentemente l’uno dall’altro (dove si supponga che LA sia misurato continuamente). Inoltre,si supponga che alcuni ricercatori duplichino le ricerche di altri ricercatori (standing-on-toes effect) e per catturare questoeffetto, si supponga che si verifichino nuove scoperte come se il numero effettivo di ricercatori fosse uguale a 𝐿^λ (con 0 ≤ λ ≤ 1). Perciò, per θ > 0 la funzione di produzione della conoscenza aggregata è data da:

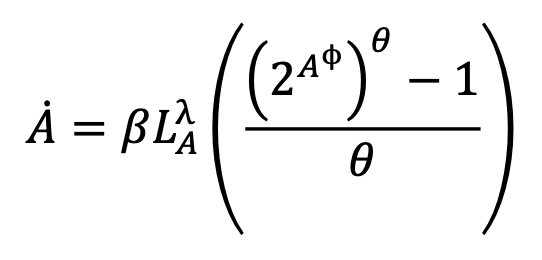(3)

Al fine di capire (dati i valori di A e LA) in che modo un aumento di θ influenza il tasso di scoperta di nuove conoscenze,𝐴̇, si osservi la derivata parziale di 𝐴̇ rispetto a θ:

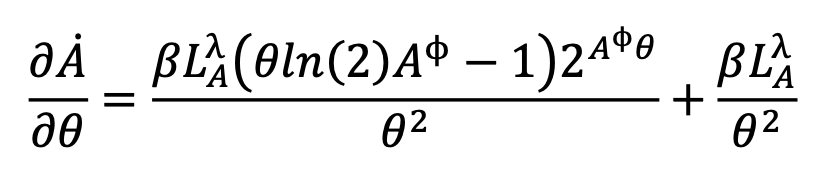(4)

È condizione sufficiente affinché questa derivata sia positiva che il termine tra parentesi sia maggiore di zero, ovvero:

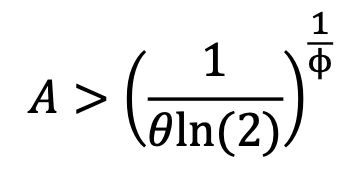(5)

La Figura 2 mostra un esempio di come 𝐴̇ vari con θ a seconda dei valori assunti da 𝛟. In particolare, si può osservare che valori più alti di θ sono associati a un tasso di crescita più veloce. Inoltre, la figura mostra come θ e 𝛟 interagiscano positivamente. Infatti, un accesso maggiore alla conoscenza (ovvero un valore alto di 𝛟) aumenta il guadagno associato ad un aumento del valore di θ.

Tuttavia, si supponga, che θ evolva con A (ovvero lo stock di conoscenza totale presentenel mondo) e quindi un A più grande implica uno spazio di scoperta più ampio e complesso. In aggiunta, si supponga che, a causa dell’aumento dell’esplosione combinatoria causato dal crescere di A, questa complessità sia destinata a sopraffare qualsiasi tecnologia IA in grado di supportare il processo di scoperta.

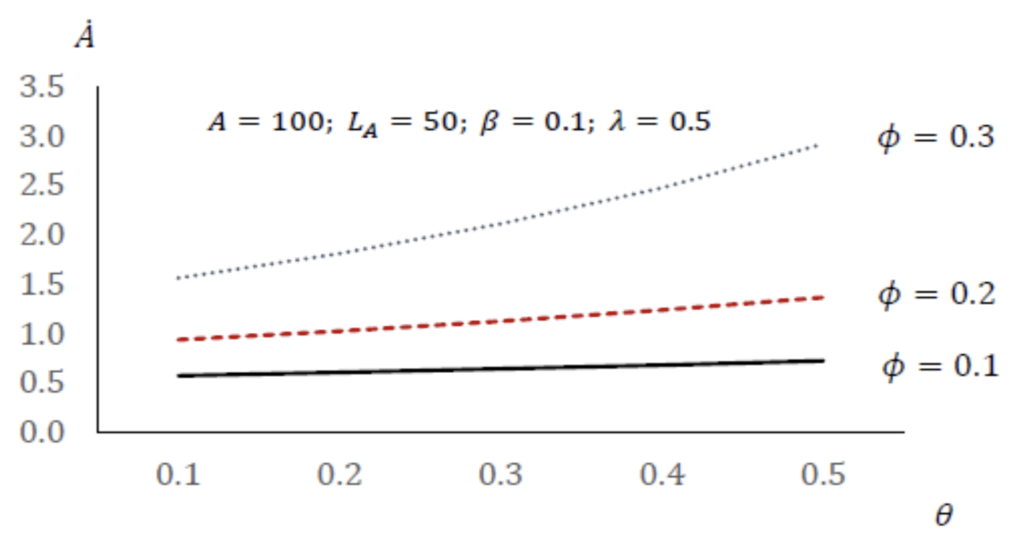
Figura 2 – Relazione tra la nuova produzione di conoscenza, θ e 𝜙 [Fonte: Ajay Agrawal, John McHale, e Alexander Oettl].

Nel modello, si tiene conto di questo assumendo che θ sia una funzione decrescente di A; cioè, θ = θ(𝐴), dove θ'(𝐴) < 0.E se A va all’infinito, si assuma che θ(𝐴) vada a zero, ovvero:

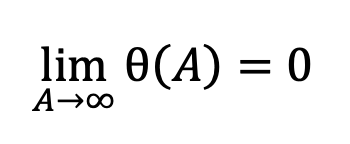(6)

Ciò significa che la funzione di scoperta converge asintoticamente (data la crescita di A) a:

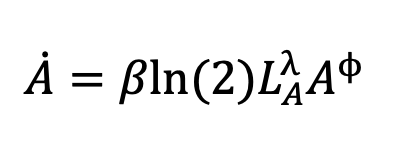(7)

Ora, al fine di comprendere l’impatto sul sistema economico derivante dal supporto dell’IA ai processi di ricerca e discoperta, si supponga che il sistema economico sia composto da due settori: quello beni finali e quello della ricerca. In particolare:

• Il settore dei beni finali utilizza per produrre la manodopera (LY) e i beni intermedi;
• Ogni nuova idea supporta la progettazione di un bene intermedio che viene realizzato attraverso l’impiego del capitale K;
• La forza lavoro totale, L, è completamente divisa tra il settore dei beni finali e quello della ricerca, così che LY + LA = 𝐿.
• La forza lavoro è uguale a tutta la popolazione esistente e cresce al ritmo 𝑛 > 0.

La funzione di produzione dei beni finali può essere scritta come:

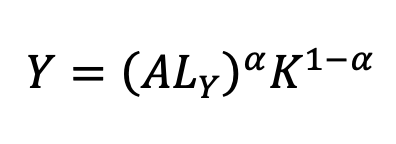(8)

dove Y è il bene finale. La funzione di utilità intertemporale di un consumatore (che tiene conto della decisione dell’individuo di allocare il consumo tra il presente e il futuro) è data da:

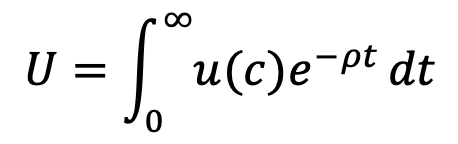(9)

dove c indica il consumo pro-capite e ρ è il tasso di sconto del consumatore (ovvero la propensione del consumatore a preferire il consumo presente rispetto a quello futuro).

Inoltre, il tasso di crescita stazionario di questa economia lungo un percorso di crescita equilibrato con crescita esponenziale costante è dato da:

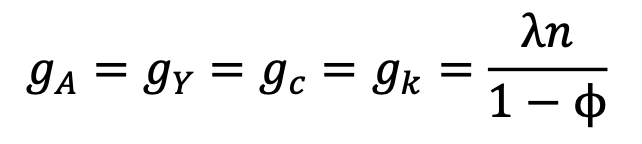(10)

dove 𝑔𝐴= 𝐴̇ 𝐴 è il tasso di crescita dello stock di conoscenza, 𝑔𝑌 è il tasso di crescita dell’output pro-capite y (con 𝑦 = 𝑌/L), 𝑔𝑐 è il tasso di crescita del consumo pro-capite 𝑐 (con 𝑐 = 𝐶/L ), e 𝑔𝑘 è il tasso di crescita del rapporto capitale-lavoro (con 𝑘 = 𝐾/L).

Fatta questa descrizione del modello, si osservi ora come i cambiamenti nei parametri della funzione di produzione della conoscenza (3) influenzano le dinamiche della crescita nell’economia. Ovvero:

• A seguito di un aumento della disponibilità delle tecnologie AI-based che migliorano l’accesso alla conoscenza da parte del ricercatore (come ad esempio Google, Meta^α, BenchSci, ), dovrebbe verificarsi un aumentodel valore di 𝛟 (ovvero alla conoscenza). Osservando l’equazione (10), un aumento di 𝛟 genera un aumento del tasso di crescita stazionario dell’economia;
• A seguito di un aumento della disponibilità delle tecnologie AI-based che migliorano il parametro relativo alla scoperta, β, e poiché β non appare nell’equazione (10), il tasso di crescita stazionario non viene modificato. Tuttavia, il miglioramento di β fa aumentare il tasso di crescita del percorso che porta stato stazionario;
• A seguito di un aumento del parametro θ dettato dalla scoperta di una nuova tecnologia AI-based e nel caso in cui l’economia sia inizialmente in uno stato stazionario, lo stato stazionario dell’economia non viene influenzato. Questo è dovuto all’assunzione fatta per l’equazione (6) secondo la quale θ convergerà a zero in quanto la complessità derivante dall’esplosione combinatoria della conoscenza travolgerà la nuova tecnologia IA. Tuttavia, anche in questo caso le dinamiche di transizione sono abbastanza diverse. Infatti, un aumento di θ influenza il percorso da seguire per arrivare allo stato stazionario a causa dei maggiori aumenti della conoscenza disponibile lungo il percorso.

Conclusioni

In conclusione, sono due le osservazioni chiave che motivano il modello sviluppato sopra.

In primo luogo, usando come analogia quella di trovare un ago in un pagliaio, gli ostacoli al processo di scoperta dei diversi domini scientifici e tecnologici nascono dalle relazioni non lineari di causa-effetto presenti tra l’enorme quantità di dati presenti.

In secondo luogo, i progressi negli algoritmi come la machine learning, offrono il potenziale per trovare conoscenzerilevanti e per prevedere combinazioni di conoscenze che produrranno nuove scoperte.

Quindi, l’apparente velocità con cui la machine learning viene applicata nei diversi ambiti, suggerisce che questa possa rappresentare una meta- tecnologia innovativa utilizzabile per la previsione di nuove combinazioni di conoscenze inspazi molto complessi rivoluzionando drasticamente il mondo della ricerca e della scoperta.

Pertanto, sebbene il principale scopo di questo modello sia esplorare come le innovazioni dell’IA possano influenzare lacrescita economica, la funzione di produzione della conoscenza sviluppata può essere potenzialmente applicata per altri scopi. Infatti, questo modello, attraverso un cambiamento concettuale, permette di modellare la scoperta come un processo operante in uno spazio costituito da numerose combinazioni.

In particolare, la funzione di produzione della conoscenza focalizza l’attenzione sulla metodologia seguita nel processo di scoperta di nuova conoscenza combinando la conoscenza esistente. Questo spostamento di enfasi è motivato dalmodo in cui la machine learning può supportare la scoperta permettendo ai ricercatori di scoprire combinazioni altrimenti difficili da individuare.

Bibliografia

• VV. (2018), “Intelligenza artificiale per le imprese: tutti i vantaggi per il futuro delle aziende”,https://www.insidemarketing.it/intelligenza-artificiale-le-imprese-tutti-vantaggi-futuro-delle-aziende/
• VV. (2018), “Intelligenza artificiale, ecco come cambia il business”, https://www.wired.it/economia/business/2017/11/24/intelligenza-artificiale-business-2/
• VV. (2018), “Intelligenza Artificiale: cos’è, come funziona e a cosa serve?”,http://www.intelligenzaartificiale.it/
• VV. (2018), “Reti Neurali”, http://www.intelligenzaartificiale.it/reti-neurali/
• Acemoglu e Restrepo P. (2018), “Modeling Automation”, https://economics.mit.edu/files/14861
• Aghion , Jones. B.E. e Jones C.I. (2017), “Artificial Intelligence and Economic Growth ”,https://web.stanford.edu/~chadj/AI.pdf
• Agrawal , McHale J. e Oettl A., (2018), “ Artificial Intelligence and Recombinant Growth”, http://www.nber.org/chapters/c14024.pdf
• Angelini (2017), “Intelligenza Artificiale e governance. Alcune riflessioni di sistema”, http://www.sipotra.it/wp-content/uploads/2017/10/Intelligenza- artificiale-e-governance.-Alcune-riflessioni-di-sistema.pdf
• Brynjolfsson e McAfee A. (2011), “ Why Workers Are Losing the War Against Machines?”, https://www.theatlantic.com/business/archive/2011/10/why-workers-are- losing-the-war-against-machines/247278/
• Brynjolfsson , Rock D. e Syverson C. (2017), “ Artificial Intelligence and the Modern Productivity Paradox: A Clash of Expectations and Statistics”, http://www.nber.org/chapters/c14007.pdf
• Dorn (2015), “The Rise of the Machines How Computers Have Changed Work”,https://www.ubscenter.uzh.ch/assets/publicpapers/PP4_the_rise_of_the_machines.pdf
• Graetz e Michaels G. (2015), “ Robots at Work”, http://cep.lse.ac.uk/pubs/download/dp1335.pdf
• Harris , Kimson A. e Schwedel A. (2018), “ Labor 2030: the collision of demographics, automationand inequality ”, http://www.bain.com/publications/articles/labor-2030-the-collision-of-demographics-automation-and-inequality.aspx
• Jin Z. (2018), “Artificial Intelligence and Consumer Privacy”, http://www.nber.org/chapters/c14034.pdf
• Korinek e Stiglitz J.E. (2017), “ Artificial Intelligence and Its Implications for IncomeDistribution and Unemployment” http://www.nber.org/chapters/c14018.pdf
• Maci (2018), “Intelligenza Artificiale, che cos’è e perché trasformerà le aziende”,https://www.economyup.it/startup/intelligenza-artificiale-che-cos-e-e-perche-trasformera-le-aziende/
• Milgrom R. e Tadelis S. (2018), “ How Artificial Intelligence and Machine Learning Can ImpactMarket Design ”, http://www.nber.org/chapters/c14008.pdf
• Purdy e Daugherty P. (2016), “ Why Artificial Intelligence is the Future of Growth”,https://www.accenture.com/t20170927T080049Zw/us-en/_acnmedia/PDF-33/Accenture-Why-AI-is-the-Future-of-Growth.PDFla=en